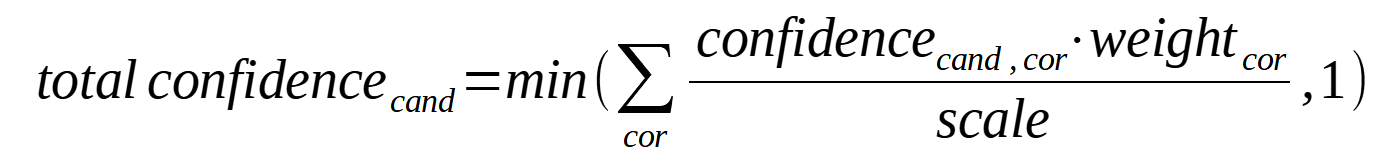
Rule Composition

Last modified 16 Jan 2024 08:28 +01:00
Table of Contents

Correlators (Correlation Rules)

The basic element of the correlation configuration is the definition of correlation rules (or correlators).

The correlation rule is more user-oriented term, while correlator is more implementation-oriented one. See also the overview document. Risking a bit of confusion, let us use the term correlator in this document.

Correlators are hierarchical, with a specified default algorithm for combining their results.

Currently, we support only the flat hierarchy: a composite correlator defined on top, with component correlators right beneath it. Please see Limitations section at the end of this document.

Confidence Values

The result of the correlator(s) evaluation is a set of candidates, each with a confidence value.

A confidence value indicates how strongly the correlator(s) believe that this candidate is the one we are looking for. It is a decimal number from the interval of (0, 1]: This means that it should be greater than zero (otherwise, the candidate would not be listed at all), and can be as large as 1. By default, the value of 1 means that the correlator is sure that this is the candidate it has been looking for.

Composition Algorithm Outline

How is the result determined?

Individual correlators are evaluated in a defined order (see Tiers and Rule Ordering).

Each correlator produces a set of candidates having zero, one, or more objects. Each candidate has a (local) confidence value from the interval of (0, 1]. Each correlator has its own weight that is used as a multiplication factor for the local confidence values produced by the correlator. (For convenience, a global scale can be defined. It can be used to re-scale the confidence values to the interval of (0, 1].)

After the evaluation, a union of all candidate sets is created, and the total confidence for each candidate is computed:

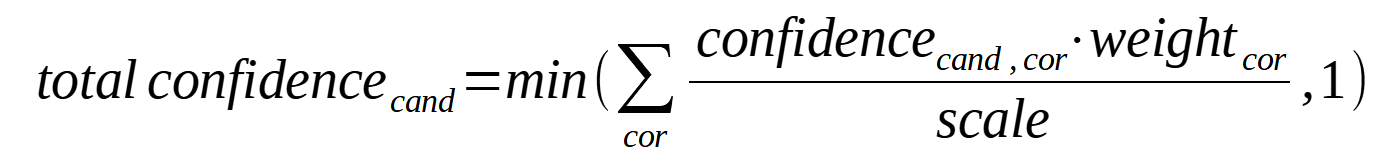
Confidence formula

Where

  • total confidencecand is the total confidence for candidate cand (being computed),

  • confidencecand,cor is the confidence of candidate cand provided by the correlator cor,

  • weightcor is the weight of the correlator cor in the composition (it is a parameter of the composition; default is 1),

  • scale is the scale of the given composition (it is a parameter of the composition; default is 1).

A Naive Example

Rules

Let us have the following rules:

Table 1. Sample set of correlation rules
Rule name Rule content Weight

name-date-id

Family name, date of birth, and national ID exactly match.

1.0

names-date

Given name, family name, and date of birth exactly match.

0.4

id

The national ID exactly matches.

0.4
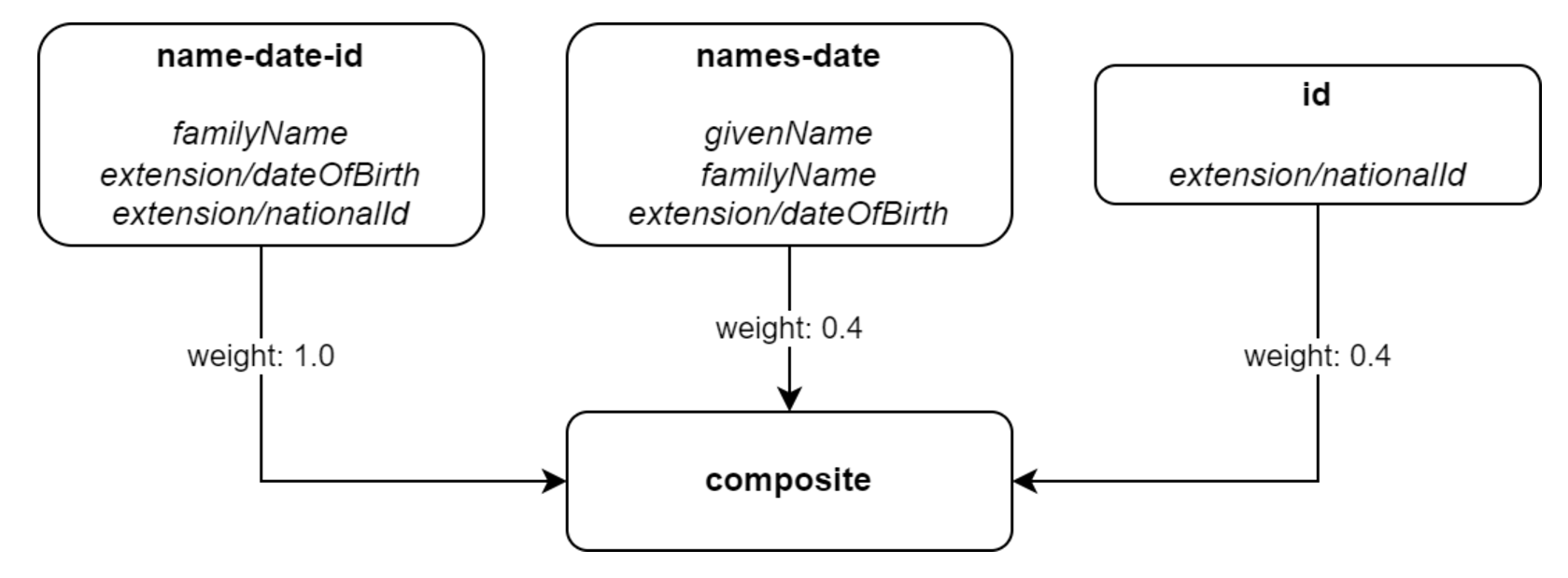
A naive example
Figure 1. Graphic representation of the sample set of correlation rules

Configuration

Listing 1. Configuration defining the sample set of correlation rules
<correlators>
    <items>
        <name>name-date-id</name>
        <item>
            <ref>familyName</ref>
        </item>
        <item>
            <ref>extension/dateOfBirth</ref>
        </item>
        <item>
            <ref>extension/nationalId</ref>
        </item>
        <!-- Weight of 1.0 is the default -->
    </items>
    <items>
        <name>names-date</name>
        <item>
            <ref>givenName</ref>
        </item>
        <item>
            <ref>familyName</ref>
        </item>
        <item>
            <ref>extension/dateOfBirth</ref>
        </item>
        <composition>
            <weight>0.4</weight>
        </composition>
    </items>
    <items>
        <name>id</name>
        <item>
            <ref>extension/nationalId</ref>
        </item>
        <composition>
            <weight>0.4</weight>
        </composition>
    </items>
</correlators>

Example Computation

Let us assume we are correlating Ian Smith, 2004-02-06, 040206/1328 and the candidate is John Smith, 2004-02-06, 040206/1328.

  • The name-date-id correlator matches with a local confidence of 1.0. Having weight of 1.0, the overall confidence increment is 1.0.

  • The names-date correlator does not match. Therefore, there is no confidence increment from it.

  • The id correlator matches with a local confidence of 1.0. Having weight of 0.4, the overall confidence increment is 0.4.

The total confidence is 1.4, cropped down to 1.0.

Table 2. Computation in a tabular form
Step Rule Matching Local confidence Weight Confidence increment Total so far

1.

name-date-id

Smith, 2004-02-06, 040206/1328

1.0

1.0

1.0

1.0

2.

names-date

-

-

0.4

-

1.0

3.

id

040206/1328

1.0

0.4

0.4

1.4 → 1.0

"Ignore if Matched by" Flag

After a quick look, we see that the match of the rule name-date-id implies the match of the rule id. Hence, each candidate matching name-date-id gets a confidence increment 1.4. This is, most probably, not the behavior that we expect. (While not necessarily incorrect, it is quite counter-intuitive.)

Therefore, midPoint has a mechanism to mark rule id as ignored for those candidates that are matched by rule name-date-id before.

Configuration

This is done by setting ignoreIfMatchedBy like here:

Listing 2. Ignoring id rule for candidates matching name-date-id
<correlators>
    ...
    <items>
        <name>id</name>
        <item>
            <ref>extension/nationalId</ref>
        </item>
        <composition>
            <weight>0.4</weight>
            <ignoreIfMatchedBy>name-date-id</ignoreIfMatchedBy>
        </composition>
    </items>
</correlators>

Example Computation

Now, when correlating Ian Smith, 2004-02-06, 040206/1328 with the candidate being John Smith, 2004-02-06, 040206/1328,

  • The name-date-id correlator matches with a local confidence of 1.0. Having weight of 1.0, the overall confidence increment is 1.0.

  • The names-date correlator does not match.

  • The id correlator matches with a local confidence of 1.0. However, it is ignored, because of the match of name-date-id.

The total confidence is thus 1.0.

Table 3. Computation in a tabular form
Step Rule Matching Local confidence Weight Confidence increment Total so far

1.

name-date-id

Smith, 2004-02-06, 040206/1328

1.0

1.0

1.0

1.0

2.

names-date

-

-

0.4

-

1.0

3.

id

040206/1328

1.0

0.4

(ignored)

1.0

Tiers and Rule Ordering

Looking at our previous example, we feel that after rule name-date-id is evaluated and finds exactly one candidate (John Smith) with the confidence of 1.0 (certain match), we can stop right there. We don’t need to evaluate any other rules. For such situations, rules can be grouped into tiers and even ordered within them.

In our particular example, we will put the first rule into a separate tier with the number of 1. The other rules will be put into tier 2.

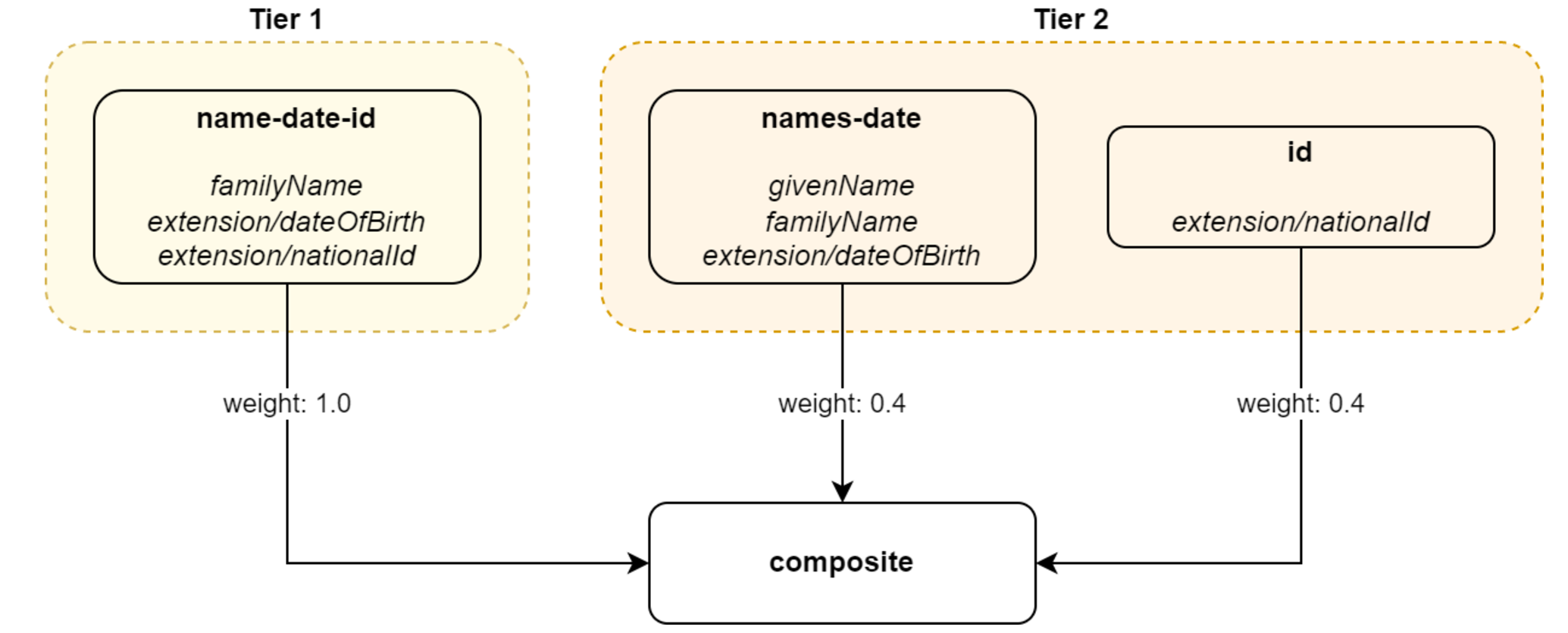
Tiers

The overall algorithm is the following:

  1. Tiers are processing sequentially, from the lower numbers to the higher ones. The unnumbered tier - if present - is evaluated last.

  2. All correlators in a given tier are processed. Their order can be specified using explicit order property (usually need not be used). Unspecified order means "last". Correlators with the same order are sorted according to their dependencies given by ignoreIfMatchedBy information.

  3. After each tier is processed, we look if we have exactly one certain candidate. (See Using the Resulting Confidence Values.) If we do, we finish the computation. If there is no certain candidate, we continue. We continue also in case there are multiple certain candidates, although this situation indicates there is something wrong with the correlation rules.

Configuration

Listing 3. Dividing the computation into tiers
<correlators>
    <items>
        <name>name-date-id</name>
        <documentation>
            If key attributes (family name, date of birth, national ID) exactly match,
            we are immediately done. We ignore given name here.
        </documentation>
        <item>
            <ref>familyName</ref>
        </item>
        <item>
            <ref>extension/dateOfBirth</ref>
        </item>
        <item>
            <ref>extension/nationalId</ref>
        </item>
        <composition>
            <tier>1</tier>
        </composition>
    </items>
    <items>
        <name>names-date</name>
        <documentation>If given and family name and the date of birth match, we present an option to the operator.</documentation>
        <item>
            <ref>givenName</ref>
        </item>
        <item>
            <ref>familyName</ref>
        </item>
        <item>
            <ref>extension/dateOfBirth</ref>
        </item>
        <composition>
            <tier>2</tier> (1)
            <order>10</order> (2)
            <weight>0.4</weight>
        </composition>
    </items>
    <items>
        <name>id</name>
        <documentation>If national ID matches, we present an option to the operator.</documentation>
        <item>
            <ref>extension/nationalId</ref>
        </item>
        <composition>
            <tier>2</tier> (1)
            <order>20</order> (2)
            <weight>0.4</weight>
        </composition>
    </items>
</correlators>
1 Tier number for the last tier can be omitted.
2 The order within the tier (can be ommited).

Note that it is not necessary to specify the last tier, that is number 2 in this case. It is because unnumbered tier always goes last.

Also, ordering within a single tier is usually not needed. This case is no exception. We provide ordering information just as an illustration how it can be done.

Example Computation

Now, when correlating Ian Smith, 2004-02-06, 040206/1328 with the candidate being John Smith, 2004-02-06, 040206/1328,

  • The name-date-id correlator matches with a local confidence of 1.0. Having weight of 1.0, the overall confidence increment is 1.0.

  • As this concludes the first tier, and a certain match was found, the processing stops here.

Table 4. Computation in a tabular form
Step Rule Matching Local confidence Weight Confidence increment Total so far

1.

name-date-id

Smith, 2004-02-06, 040206/1328

1.0

1.0

1.0

1.0

Evaluation of other rules is skipped

Using the Resulting Confidence Values

The resulting aggregated confidence values for individual candidates are compared with two threshold values:

Table 5. Threshold values
Value Description

Definite match threshold (DM)

If a confidence value is equal or greater than this one, the candidate is considered to definitely match the identity data. (If, for some reason, multiple candidates do this, then human decision is requested.)

Candidate match threshold (CM)

If a confidence value is below this one, the candidate is not considered to be matching at all - not even for human decision.

Said in other words:

  1. If there is a single candidate with confidence value ≥ DM then it is automatically matched.

  2. Otherwise, all candidates with confidence value ≥ CM are taken for human resolution.

  3. If there are none, "no match" situation is assumed.

Default values

Table 6. Default values for the thresholds
Threshold Default value

Definite match (DM)

1.0

Candidate match (CM)

0.0

Configuration

Listing 4. Setting the thresholds
<correlation>
    <correlators>
        ...
    </correlators>
    <thresholds>
        <definite>0.75</definite>
        <candidate>0.25</candidate>
    </thresholds>
</correlation>

Limitations

Although it is possible to configure arbitrary combination of the correlators, and such a combination will most probably work, for practical reasons there are the following limitations of what is "officially" supported. Everything beyond this is considered to be experimental functionality:

  1. ID Match correlator cannot be combined with other correlators.

  2. Filter-based correlators cannot be combined with the other ones.

  3. Expression-based correlators are experimental altogether.

  4. Composite correlator can be provided at the top level only. (It is the implicit instance of the composite correlator that is not visible in the correlation definition. It is represented by the root correlators configuration item.)

Said in other words, only the items correlators can be combined. The use of other ones in the composition is considered experimental.

Was this page helpful?
YES NO
Thanks for your feedback