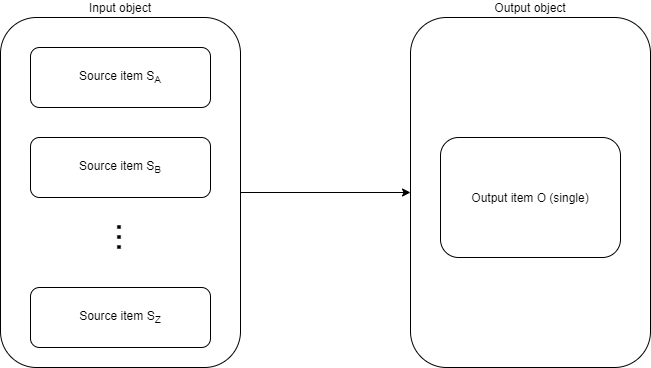
Metadata mapping model

Last modified 03 Jul 2024 14:42 +02:00

Data mapping

Data mappings transform source item(s) - e.g. S_A, S_B, …, S_Z - to output (target) item - e.g. O - in the context of a single object.

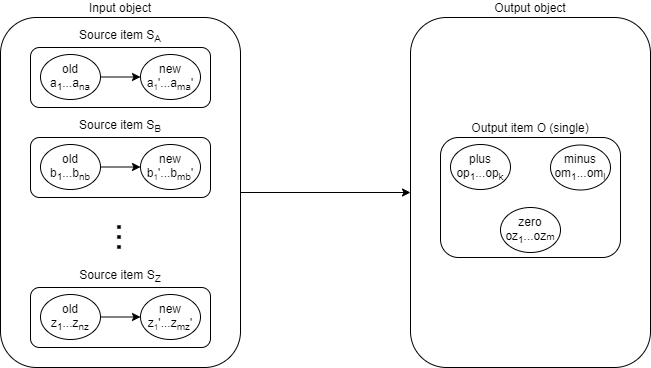
Each source has some old and new values. Let us denote them a₁, a₂, …, a_na → a₁', a₂', … , a_ma' for source S_A, and similarly for other sources.

The output consists of plus, minus and zero set of values, denoted op₁, op₂, …, op_k for plus, om₁, om₂, …, om_l for minus, and oz₁, oz₂, …, oz_m for zero set.

So the above picture can be augmented with the values like this:

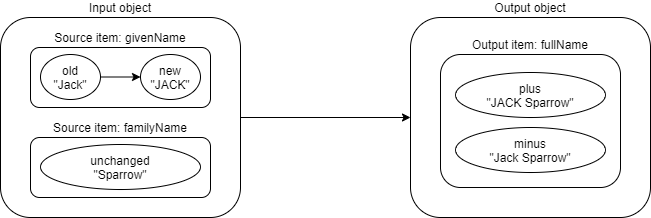
An example:

Why is there only one source object? In fact, with the advent of linked objects one can imagine a mapping that would operate on a set of all objects connected to the focus via particular link type. See Multi-objects mappings.

If we use combinatorial evaluation (this is the case for most of the time) the values are constructed like this:

i.e. output value o_j (or, sometimes, more values e.g. o_k, o_l, …) are computed from values a_ia, b_ib, …, z_iz from sources S_A, …, S_Z, respectively, taking a combination of i_a, …, i_z-th value from respective value sets of these sources. (It is also possible that the set of output values for an input combination is empty.)

An example:

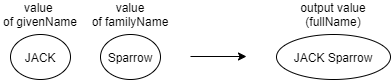
Metadata mapping

Here we have to start thinking of metadata.

We need to compute metadata for each of the output values produced. For simplification, we can assume that if a mapping produces more than one output value for a given combination of input values, all of them will get the same metadata. Therefore, we can restrict our thinking to metadata for single output value.

From the metadata point of view it is not important if the (data) values are being added or kept unmodified by the mapping. The only thing we look at is that we want to skip computing metadata for values that go into the output minus set. ^[1]

Metadata for given value are organized into items just like ordinary data in objects are. Standard data mappings reference their sources and target as items. It is natural for metadata mappings to do the same. In this way we could have partial mappings for (e.g.) level of assurance item, confidentiality item, creation time item, and so on. These mappings can be applied independently (and selectively, if needed), just like ordinary mappings are applied to data objects.

There are some differences, though.

While for standard data mapping we have exactly one input object, for metadata mappings we have multiple input metadata collections. For each input data value there is separate metadata. (Represented as a set of metadata items. Technically, metadata is represented by prism container value.)
At the metadata level we have no deltas. An input value (kept unchanged or being added) has its own metadata, and this metadata is immutable. It was attached to the value when the value was created, and will never be changed. (As the value itself does not change. It can be created or deleted, but never changed.) ^[2] ^[3]

Metadata mapping model

So, we have a situation where we combine input values a, b, …, z from sources S_A, S_B, …, S_Z into an output value. (For example, S_A = givenName, S_B = familyName, output = fullName).

A metadata mapping has sources and output just like ordinary data mapping. However, sources do not reference S_A, S_B, …, S_Z. They are orthogonal to data mapping sources. Metadata mapping sources reference metadata items, like level of assurance, confidentiality, value origin, creation time, and so on. Each source corresponds to a single metadata item, just like mapping source corresponds to a single object item. Also, the output corresponds to a single metadata item; just like in mappings.

So, for example, our metadata mapping can have two sources: loa (level of assurance) and source (source system) and one output loa (resulting level of assurance). The rule could be simple: take the lowest level of assurance of all inputs. However, if source is socialLogin then override the computation and use loa of unknown. (This example is weird. It is here only to demonstrate metadata mapping with two sources.)

<metadataMapping>
    <source>
        <path>loa</path>
    </source>
    <source>
        <path>source</path>
    </source>
    <expression> ... </expression>
    <target>
        <path>loa</path>
    </target>
</metadataMapping>

Example evaluation:

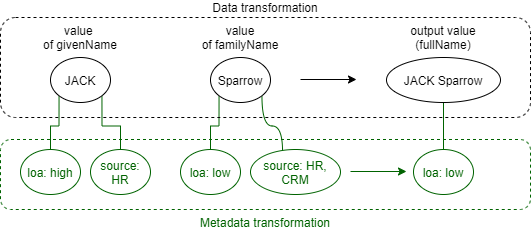
(Again, normally single familyName value would not have two sources. Here it has just for illustration purposes.)

Looking at metadata evaluation only:

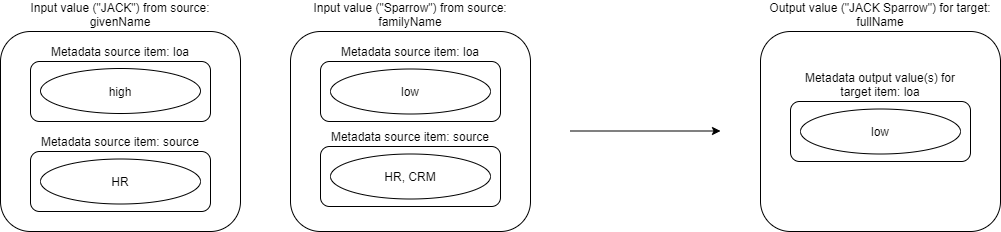
And, if we slightly generalize this picture, we get the following:

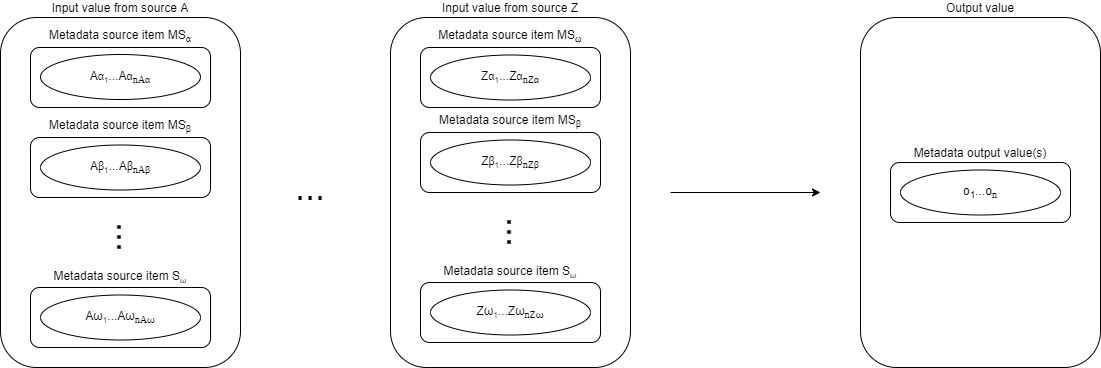
Note that sources are marked S_A, S_B, …, S_Z, whereas metadata sources are orthogonal. For the lack of invention let’s mark them MS_α, MS_β, …, MS_ω. Input values for metadata transformation are then given by the matrix (shown here as table):

Table 1. Metadata-data source matrix
Data/metadata source	Source A	Source B	…	Source Z
MS α	Aα₁, Aα₂, …	Bα₁, Bα₂, …	…	Zα₁, Zα₂, …
MS β	Aβ₁, Aβ₂, …	Bβ₁, Bβ₂, …	…	Zβ₁, Zβ₂, …
…	…	…	…	…
MS ω	Aω₁, Aω₂, …	Bω₁, Bω₂, …	…	Zω₁, Zω₂, …

Imagine we want to compute output values using a Groovy (or JavaScript, Python, etc.) script. What variables will the script expect?

General case (detailed information)

If the script would like to consider the whole situation, it would need to obtain the whole matrix. For example, it would need to know that

value of JACK for data source givenName has loa of high and source of HR,
value of Sparrow for data source familyName has loa of low and source of HR and CRM.

This information is simply accessible from the data values (JACK, Sparrow) if they are represented as PrismValue objects - via valueMetadata() or similar method.

Simplified case (summarization on metadata source items)

However, often we want simply gather all values for specified metadata item and process them as set. Referring to our example, we would like to know that:

loa = { high, low }
source = { HR, CRM }

The mapping would then look like this:

<expression>
    <script>
        <code>
            source.contains('socialLogin') ? 'unknown' : custom.minLoa(loa)
        </code>
    </script>
</expression>

We assume that custom.minLoa is a function that takes a collection of LoA values and returns the lowest one of them.

In the notation of Metadata-data source matrix we can define the variables as:

α = { Aα₁, Aα₂, … , Bα₁, Bα₂, …, Zα₁, Zα₂, … }
β = { Aβ₁, Aβ₂, … , Bβ₁, Bβ₂, …, Zβ₁, Zβ₂, … }
…
ω = { Aω₁, Aω₂, … , Bω₁, Bω₂, …, Zω₁, Zω₂, … }

for metadata sources α, β, …, ω.

Combinatorial evaluation?

Does it make sense to think about combinatorial evaluation of metadata values? I.e. something like:

JACK - loa high - source HR - Sparrow - loa low - source HR → o1
JACK - loa high - source HR - Sparrow - loa low - source CRM → o2

and then using o1 and o2 as a set of output values for resulting level of assurance?

Again, referring to Metadata-data source matrix we would create script inputs as:

Aα = Aα_iAα
Aβ = Aβ_iAβ
…
Aω = Aω_iAω
Bα = Bα_iBα
Bβ = Bβ_iBβ
…
Bω = Bω_iBω
…
Zα = Zα_iZα
Zβ = Zβ_iZβ
…
Zω = Zω_iZω

For all possible combinations of indices i_Aα, i_Aβ, …, i_Zω.

In our example, A = givenName with JACK value, B = familyName with Sparrow value, α = loa, β = source, so

Aα (givenName/loa) ∈ { high }
Aβ (givenName/source) ∈ { HR }
Bα (familyName/loa) ∈ { low }
Bβ (familyName/source) ∈ { HR, CRM }

So, is this important and worth implementing? Maybe. Let us just remember this option to eventually implement it when needed.

1. Even this is questionable. Consider e.g. assigned focus mappings for an assignment that is being deleted. We have to review such a situation eventually.

2. What about container value e.g. assignment modifications? Can we view that as value deletion and creation operations?

3. Also interesting is the following use case: Have information about provisioning targets for data. Know where the data are provisioned to or where they were provisioned in the past. This would probably require modifications of metadata in the opposite direction, i.e. going from outputs to source values.

Was this page helpful?

YES NO

Thanks for your feedback